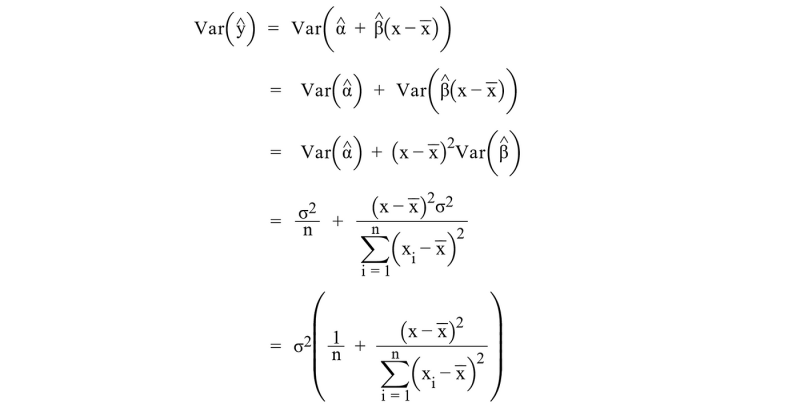Rumus Interval

Rumus Interval – Dalam non-probability sampling, item yang digunakan sebagai sampel dipilih tanpa mempertimbangkan nilai probabilitasnya Convenience sampling  item dipilih karena alasan kenyamanan, seperti efektivitas biaya dan kemudahan akses. Judgment sample  objek dipilih berdasarkan pendapat ahli Snowball sample  digunakan apabila anggota populasinya sedikit diketahui, maka dilakukan upaya untuk menggali informasi dari sampel yang diketahui untuk mendapatkan sampel selanjutnya untuk mendapatkan ukuran sampel yang lebih besar.

5 Probability sampling Dalam probability sampling, objek dipilih sebagai sampel dengan memperhatikan nilai probabilitas Probability sample Simple random stratified cluster sistematis

Table of Contents

Setiap individu dalam populasi mempunyai kesempatan yang sama untuk dipilih sebagai sampel. Sampel diperoleh secara acak dengan bantuan tabel bilangan acak atau random number generator atau dengan cara undian.

Pengertian Skala Likert Dan Contoh Cara Hitung Kuesionernya

Bagi kerangka sampel N individu menjadi n kelompok dengan k anggota: k=N/n Pilih secara acak satu individu dari kelompok 1 Kemudian pilih setiap k individu Kelompok pertama N = 40 n = 4 k = 10

8 Sampel bertingkat Membagi populasi menjadi dua atau lebih subkelompok (disebut strata) dengan karakteristik tertentu. Lakukan pengambilan sampel acak sederhana untuk setiap strata secara proporsional Gabungkan sampel yang diperoleh dari setiap strata Populasi dibagi menjadi 4 strata

9 Cluster Sampling Populasi dibagi menjadi beberapa cluster yang mewakili populasi. Melakukan simple random sample untuk cluster yang terbentuk Populasi dibagi menjadi 16 cluster Sampel dipilih secara acak

10 Rumus Slovin Salah satu rumus yang digunakan untuk menentukan ukuran sampel adalah semakin besar toleransi kesalahan (e), semakin kecil ukuran sampel. Dimana: n = ukuran sampel N = ukuran populasi e = toleransi kesalahan (0<e<1)

Materi Simpangan Rata Rata Lengkap Dengan Rumus, Penerapan Dan Contohnya

Jelaskan dan jelaskan metode pengambilan sampel berikut Purposive sampling Quota sampling Voluntary sampling Kumpulan manajer perusahaan yang bonafid terdiri dari 150 anggota, 100 di antaranya adalah manajer junior dan sisanya adalah manajer senior. Tentukan ukuran sampel jika Anda menginginkan toleransi kesalahan 0,25. Berapa banyak sampel masing-masing manajer junior dan manajer senior jika digunakan teknik stratified sampling?

Estimasi titik adalah nilai tunggal Interval kepercayaan memberikan informasi tambahan tentang varian estimasi Batas kepercayaan atas Batas kepercayaan lebih rendah Estimasi titik Lebar interval kepercayaan Bab 8-12

Mempertimbangkan variasi statistik dari setiap sampel berdasarkan data 1 sampel Memberikan informasi tentang kedekatan nilai estimasi dengan nilai sebenarnya dari parameter Dinyatakan sebagai tingkat kepercayaan (confidence level) Misalnya 95% confidence atau 99% percaya diri Tidak pernah percaya diri 100% 8-14

Saya memiliki keyakinan 95% bahwa nilai μ adalah antara 40-60. Populasi sampel acak Rata-rata X = 50 (rata-rata, μ, tidak diketahui) Contoh Bab 8-15

Soal Data Dibawah Ini Menyatakan Usia 50 Orang Karyawan Pt Karya Mulia. {:[30,17,50,62,19,20,22

Rumus umum Rumus umum untuk semua interval kepercayaan: Estimasi titik ± (titik kritis) (Standard Error) Dimana: Estimasi titik  statistik sampel untuk pendugaan parameter populasi yang diinginkan Titik kritis  nilai distribusi sampling dari estimasi titik yang pada tingkat kepercayaan yang diberikan Standard Error standar deviasi estimasi titik

Asumsi Standar deviasi σ diketahui Populasi berdistribusi normal Jika populasi tidak normal, gunakan sampel besar (central limit theory) Estimasi interval kepercayaan: dimana estimasi titik Zα/2 adalah titik kritis distribusi normal dengan probabilitas  /2 kesalahan standar

Pertimbangkan interval kepercayaan 95%: Zα/2 = -1,96 Zα/2 = 1,96 Z unit: Batas kepercayaan bawah Batas kepercayaan atas X unit: Estimasi titik

90%, 95% dan 99% Faktor kepercayaan Zα/2 80% 90% 95% 98% 99% 99,8% 99,9% 0,80 0,90 0,95 0,98 0,99 0,998 0,998 0,98 0,98 0,98 75 3,08 3,27 Bab 8-20

Bab Iii Distribusi Data

Sampling Distribution Mean/Mean2 x Rentang interval dari x1 x2 (1-)x100% interval yang dihasilkan mengandung nilai μ; Sedangkan ()x100% tidak. Antara kepercayaan

22 Contoh Studi ini tertarik untuk mengetahui pendapatan rata-rata Manajer Pemasaran di ritel. Sampel dari 256 manajer menunjukkan bahwa pendapatan rata-rata mereka adalah satu juta euro per tahun. Deviasi standar populasi ini adalah 20,5 juta/tahun. Beberapa pertanyaan yang ingin dijawab oleh penelitian ini adalah: Apa arti populasi jika diinginkan tingkat kepercayaan 95%? Bagaimana hasil ditafsirkan? Bab 8-22

24 Interpretasi Dengan tingkat kepercayaan 95%, dapat dikatakan bahwa pendapatan rata-rata Manajer Pemasaran Ritel sebenarnya adalah sekitar – juta/tahun. Bab 8-24

Tentu saja tidak. Di dunia nyata, σ jarang diketahui. Jika ada situasi dimana σ diketahui, µ juga harus diketahui. Jika µ diketahui, kita tidak perlu repot mengumpulkan data sampel. penerbitan sebagai Prentice Hall

Cara Menghitung Interval Kepercayaan: 6 Langkah (dengan Gambar)

DCOVA Jika simpangan baku populasi σ tidak diketahui, kita dapat menggantinya dengan simpangan baku sampel S . Akibatnya, ketidakpastian meningkat karena S bervariasi antar sampel. Jadi distribusi-t digunakan sebagai pengganti distribusi normal

(di mana tα/2, db adalah titik kritis distribusi-t dengan derajat kebebasan (db) = n -1 dan masing-masing memiliki luas α/2 di setiap sisi)

30 Tabel t DCOVA α Contoh: n = db= n – 1 =  = /2 = 0.05 db .10 .05 .025 1 3.078 6.314 12.706 2 1.886 2.920 3 = 1 in.2.3033 Tabelnya adalah .2.3033 termasuk t -nilai (bukan probabilitas) t 2920 Bab 8-30

X = 50 dan S = 8. Buat selang kepercayaan 95% untuk μ db = n – 1 = 24 sehingga selang kepercayaan 95% ≤ μ ≤

Memahami Rumus Nilai Minimum Dan Maksimum

Distribusi proporsi sampel mendekati normal jika ukuran sampel cukup besar, dengan standar deviasi Standar deviasi diperkirakan dengan statistik sampel

Interval kepercayaan π dimana Zα/2 : Nilai Z untuk tingkat kepercayaan 1-α p : rasio sampel n : ukuran sampel Keterangan: Nilai X harus memenuhi X > 5 dan n – X > 5

36 Contoh Sebuah sampel acak dari 100 orang menunjukkan bahwa 25 dari mereka kidal. Tentukan interval kepercayaan 95% untuk proporsi sebenarnya dari populasi yang kidal. Bab 8-36

37 Contoh Sebuah sampel acak dari 100 orang menunjukkan bahwa 25 dari mereka kidal. Tentukan interval kepercayaan 95% untuk proporsi sebenarnya dari populasi yang kidal. np = 100 * 0.25 = 25 > 5 & n(1-p) = 100 * 0.75 = 75 > 5 Pastikan ukuran sampel mencukupi

Rumus Kecepatan Rata Rata, Jarak, Dan Waktu, Beserta Contoh Pengerjaannya

1. Lembaga penelitian tertarik untuk mengetahui berapa biaya tembakau per minggu untuk perokok aktif. Dipilih sampel acak sebanyak 49 perokok aktif yang rata-rata pengeluaran rokoknya 200 ribu/minggu. Diketahui dari penelitian sebelumnya bahwa standar deviasi populasi ini adalah 50 ribu/minggu. Buat dan interpretasikan interval kepercayaan 90% untuk rata-rata konsumsi rokok sebenarnya dari perokok aktif.

39 2. Asosiasi Industri Pertanian bertujuan untuk menentukan rata-rata konsumsi susu tahunan. Oleh karena itu, 16 orang dipilih secara acak, dimana rata-rata konsumsi susu tahunan dari 16 orang adalah 60 galon dan standar deviasinya adalah 20 galon. Buat interval kepercayaan 90% untuk rata-rata populasi dan interpretasikan.

Data Nilai Ulangan Fisika 40 Siswa Kelas Xii.

Agar situs web ini berfungsi, kami merekam data pengguna dan membaginya dengan pemroses. Untuk menggunakan situs web ini, Anda harus menerima kebijakan privasi kami, termasuk kebijakan cookie kami.4 KELOMPOK FREKUENSI Kelompokkan data ke dalam beberapa kategori dan kemudian hitung jumlah pengamatan di setiap kategori. ATAU Sesuatu yang menggambarkan frekuensi kemunculan anggota populasi yang didistribusikan oleh nilai variabel yang ditangkapnya.

5 DISTRIBUSI FREKUENSI Data hasil pengamatan disajikan dalam bentuk tabel dengan mengelompokkannya ke dalam interval untuk data yang bervariasi. Distribusi frekuensi digunakan ketika diperoleh sekelompok bahan penelitian yang tidak dapat diorganisasikan menjadi satu distribusi.

Menentukan nilai tertinggi dan terendah Menentukan rentang skor Menentukan jumlah interval kelas Menentukan panjang interval kelas Menentukan ujung bawah dan atas interval kelas pertama dan kelas lainnya Menentukan jumlah frekuensi untuk setiap interval kelas

Contoh poin data penelitian dalam ujian mata pelajaran IT untuk 60 siswa 50 75 70 65 60 55 90 80 85

Rumus Simpangan Baku

Perhatikan data penelitian dan tentukan skor tertinggi dan terendah dari data Skor tertinggi = Skor terendah =

Range = Range = (R) R = Xn – Xl Ket R = Range Xn = Titik pengamatan tertinggi Xl = Titik pengamatan terendah

Aturan Sturges KI = 1 + 3,3 log n Rabu KI = interval kelas n = jumlah pengamatan

Rumus p = R / KI Ket P = Panjang kelas interval R = Kisaran KI = Beberapa kelas interval

Soal Sebuah Fungsi Didefinisikan Dengan Rumus Y=7x+3 Y=3 7x Interval Y= 3+7x Yang Tepat Agar Fu

Pembuatan tabel distribusi frekuensi dapat dilakukan dengan urutan sebagai berikut: Distribusi frekuensi Distribusi frekuensi absolut Distribusi frekuensi relatif Distribusi frekuensi kumulatif

TABEL 1.1 DISTRIBUSI NILAI FREKUENSI TEKNOLOGI INFORMASI PADA SISWA KOMUNIKASI ANGKA GENAP 2011 No kesenjangan kelas (Jumlah poin) Frekuensi (f) 1. 2. 3. 4. 5. 6. 7. 5 3 25 – 2.9 3 3 2 TOTAL 60

TABEL 1.2 DISTRIBUSI FREKUENSI (ABSOLUT) NILAI DATA MATA KULIAH DATA KOMPUTER KOMPUTER NOMOR GANJIL 2011 Nilai Ujian Frekuensi (f abs) 49 – 54 85 – 90 5 1331

TABEL 1.3 FREKUENSI PENGETAHUAN (RELATIF) NILAI PENGETAHUAN KOMUNIKASI PENGETAHUAN SISWA ANGKA GENAP 2011 Nilai Ujian Frekuensi (f %) 49 – 54 85 – 90 8.3% 33.3% 4% 3.4% 4%

Mengenal Pengertian Median Dan Cara Menghitung Median

TABEL 1.4 ALOKASI FREKUENSI (Kumulatif) MAHASISWA MAHASISWA MAHASISWA ANGKA GENAP 2011 Nilai Ujian

Rumus interval kelas, contoh latihan interval, interval ganti oli motor, latihan interval lari, rumus confidence interval, latihan interval, interval training, contoh latihan interval training, reebok interval 96, interval qt, interval, rumus interval statistik