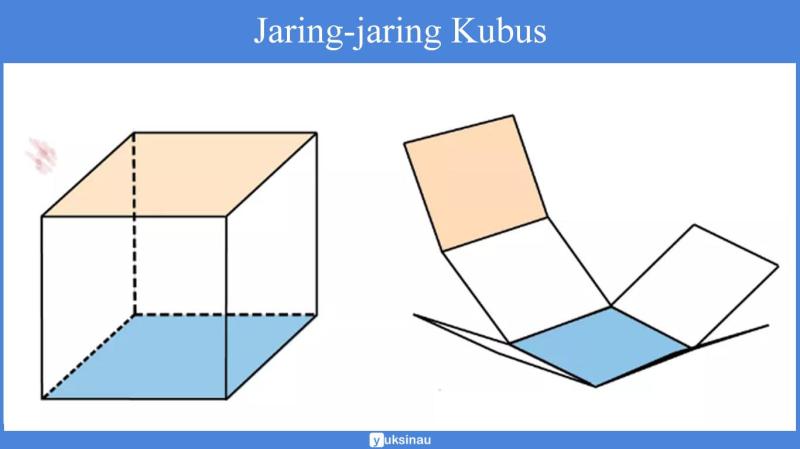
Ruas Garis Perpotongan Dua Sisi Bidang Kubus Dinamakan – Kubus ABCD.EFGH memiliki 12 rusuk: AB, BC, CD, AD, EF, FG, GH, EH, AE, BF, CG, dan DH.
Rusuk AB, BC, CD, dan AD disebut iga dasar, iga AE, BF, CG, dan DH disebut iga berdiri, dan iga EF, FG, GH, dan EH disebut iga atas.
Ruas Garis Perpotongan Dua Sisi Bidang Kubus Dinamakan
Diagonal kubus adalah segmen garis yang menghubungkan dua simpul berlawanan di bidang apa pun. Setiap bidang kubus memiliki dua diagonal.
Doc) Bab Vii Geometri Ii
Kubus ABCD.EFGH memiliki 12 bidang diagonal: AC, BD, AF, BE, AH, DE, BG, CF, CH, DG, EG, dan FH.
Diagonal ruang kubus adalah segmen garis yang menghubungkan dua titik sudut yang berlawanan di ruang mana pun. Diagonal-diagonalnya sama panjang dan berpotongan di satu titik.
Bidang yang sejajar dengan bidang visual disebut bidang frontal. dan bidang yang tegak lurus bidang bayangan disebut bidang ortogonal. Kubus ABCD.EFGH memiliki satu bidang depan: EFGH, dan empat bidang ortogonal: ADHE, BCGF, ABFE, dan CDHG. Diketahui sisi = s. Total panjang rusuk balok atau panjang rangka balok adalah
Dua garis disebut sejajar jika mereka terletak pada bidang yang sama dan tidak memiliki titik persekutuan.
Ruas Garis Yang Merupakan Diagonal Pada Kubus Abcd.efgh Adalah
Dua garis berpotongan jika mereka terletak pada bidang dan berbagi satu titik. Facet adalah area yang mengelilingi bentuk. Sisi adalah titik potong antara dua sisi. Titik sudut adalah persimpangan antara beberapa sisi. Sisi diagonalnya adalah Ruas garis yang menghubungkan dua titik sudut yang berlawanan pada sisi diagonal ruang adalah ruas garis yang menghubungkan dua titik sudut yang berlawanan pada bidang geometri. Bidang diagonal adalah bidang yang melewati dua sisi berlawanan yang tidak berada pada bidang yang sama H G E F D C A B.
Tentukan garis a. titik pada garis b titik di luar garis 2. titik pada bidang a. titik pada bidang b titik jauh dari bidang 3. garis ke garis a. berpotongan b. sejajar c. remuk d.
3 4. Baris ke pesawat Garis terletak pada bidang b. Garis sejajar c. lurus melalui bidang 5. ke bidang a. gerinda b. paralel c. pemotongan
Setara dengan kubus dengan rusuk a cm Maka luas permukaan = 6 a² cm² Volume = cm² Panjang diagonal sisi = a cm Panjang diagonal ruang = a cm H G E F D C A B
Smp8mat Matematikakonsepdanaplikasinya Dewinuharini
6 D. Prisma Prisma adalah bangun geometri yang dibatasi oleh dua bidang sejajar dan beberapa bidang yang berpotongan sepanjang garis sejajar. Dua bidang sejajar disebut bidang dasar dan bidang atas. Bidang lainnya disebut tegak lurus.
Ada tujuh jenis prisma.Prisma segi adalah prisma dengan alas sama sisi. Prisma dengan sisi belah ketupat disebut belah ketupat.Prisma dengan ujung terpotong adalah prisma yang alas dan simpulnya tidak sejajar.
8 Luas dan volume prisma Luas prisma = luas alas + luas puncak + luas kulit Volume prisma = luas alas x tinggi Contoh: Sebuah prisma memiliki 6, 8, 10 rusuk utama dan 5 rusuk vertikal Tentukan luas permukaan dan volume Jawaban: Luas permukaan = 2 x luas alas + luas cangkang = 2. ½ ( ) .5 = = 168 volume = luas alas x tinggi = ½ = 120
9 E. Limas Piramida adalah bangun geometris yang dibatasi oleh n sisi dan beberapa bidang vertikal yang berbentuk segitiga. Jenis piramida dengan piramida sisi-n adalah piramida dengan alas sisi-n sembarang dan puncak sisi-n sembarang.Piramida sisi-n biasa adalah piramida dengan alas sisi-n normal dan ujungnya menonjol di pusat alas Limas dengan alas berbentuk lingkaran disebut kerucut, luas permukaan = luas alas + luas kulit. Volume limas = luas alas x tinggi
Kubus Dan Balok Matematika Smp
Contoh Sebuah kerucut mempunyai jari-jari 6 cm dan tinggi 8 cm Tentukan luas permukaan dan volumenya Jawab: Permukaan = alas + kulit = π 6² + π.6.10 = 36π + 60π = 96π cm² Volume = luas alas x tinggi = π 6².8 = 96π cm³
Luas bayangan adalah luas gambar (buku) di depan (garis AB, garis AE) H G E F D C A B.
6. Sudut deviasi/sudut samping yaitu sudut pada citra antara garis horizontal yang mengarah ke kanan dan garis vertikal yang menghadap ke belakang (sudut BAD, sudut FEH). Panjang garis tegak lurus pada bayangan dan panjang bayangan sebenarnya (AD) : AD aktual) H G E F D C A B
Contoh: Gambarlah sebuah kubus ABCD.EFGH dengan sisi 6 cm, sudut keluar 30°, rasio proyeksi ⅓, ABFE depan dan AB horizontal.Jawaban: H G E F D C 30° B A Panjang AD pada gambar = ⅓,6 = 2 cm. .
Pengertian Garis Sejajar, Garis Berpotongan, Tegak Lurus, Dan Berimpit
Jarak antara titik A dan B adalah panjang ruas AB B A H G E F Jarak antara titik D dan H adalah a Jarak antara titik B dan G adalah a√2 D C A a B
2. Jarak dari satu titik ke titik lainnya Jarak titik A ke garis g adalah panjang ruas AP dimana titik P terletak pada garis g dan AP ┴ g A g P H H G E jarak titik A ke garis g adalah AP F T jarak titik F ke garis AB adalah FB D C C A a B A Jarak titik C ke garis AH adalah CT.
3. Jarak dari titik ke bidang Jarak titik A ke bidang α adalah panjang garis yang diproyeksikan dari titik A ke bidang α A H G E F Γ A’ α D T C Jarak A ke bidang α adalah panjang AA’ A B Jarak titik H ke bidang ABCD adalah Jarak HD Jalur dari titik B ke bidang ACGE adalah BT.
4. Jarak dari garis ke bidang Jarak garis g dan bidang α adalah panjang ruas garis tegak lurus garis g dan bidang α (panjang ruas PA) P g H G Γ A E F α bidang lurus dan sejajar D C A B Jarak dari garis GH ke bidang ABCD di CG.(Cubic Ribs)
Pdf) Modul Garis Dan Sudut
5. Jarak antara dua bidang Jarak antara dua bidang adalah panjang penampang tegak lurus kedua bidang P α ∟ H G Γ Q E ∟ F β. Jarak antara dua bidang adalah PQ DC C Γ A B. Jarak antara bidang ABCD dan EFGH adalah BF ( tepi dari kubus)
Jarak dua garis sejajar adalah panjang ruas garis yang tegak lurus P ∟ H G ∟ Q E ∟ F Jarak kedua garis adalah PQ D C Γ A B Jarak garis AB dan EF adalah BF(titik ujung kubus)
Jarak antara dua garis yang berpotongan adalah panjang ruas garis yang tegak lurus P ∟ H G ∟ Q E F Jarak antara dua garis adalah PQ ∟ D ∟ C A B Jarak antara garis AD dan CG adalah DC (pinggir kubus )
Diketahui dua titik A dan B pada garis g, proyeksikan A dan B pada bidang α, bayangan yang dihasilkan adalah A’ dan B’. Garis-garis yang melewati A’ dan B’ dihasilkan dari proyeksi garis g pada bidang α g B A’ B’ α H G Contoh: Tentukan proyeksi garis EG sepanjang bidang ABCD pada kubus Jawaban: E F D C Hasil proyeksinya adalah garis AC A B.
Modul 5 Matematika Di Sd.pptx
Adalah α (menggunakan sudut lancip) α g Contoh: Tentukan sudut antara garis AC dan garis AH (kubik) Jawaban: H G E F D Sudut yang diperlukan adalah segitiga sama sisi CAH, jadi besar sudut garis AC dan AH adalah 60º α C A B.
Jika garis g dan h berpotongan, sudut antara garis g dan h adalah sudut yang dibentuk oleh garis g’ dan h’, dengan g // g’ dan h // h’ h h’ α g’. kubus? Jawab : H G E F Sudut garis HG dan BC = < ADC = 90º D C α A B
P pilih sembarang titik P pada garis, proyeksikan P pada bidang, misal titik P’, sudut PTP’ adalah sudut antara garis dan bidang α T Γ P’, misalnya, tentukan sudut antara garis AF dan bidang ABCD pada kubus? Jawab : H G E F D Segitiga sama kaki BAF Sudut yang dimaksud adalah 45º C α Γ A B.
Ambil titik mana saja pada garis potong, seperti titik A. Dari titik A, ditarik dua garis. yang masing-masing terletak pada bidang-U dan bidang-V. dan tegak lurus garis potong Sudut BAC = α adalah sudut antara bidang u dan bidang v.
Buku Panduan Guru Matematika Untuk Smp Kelas Vii
Rumus mencari sisi kubus, rumus sisi kubus, garis edar planet dinamakan, kubus sisi, banyak sisi kubus, dua sisi, ruas garis, bentuk sisi kubus, jumlah sisi kubus, sisi pada kubus, diagonal sisi kubus, panjang sisi kubus