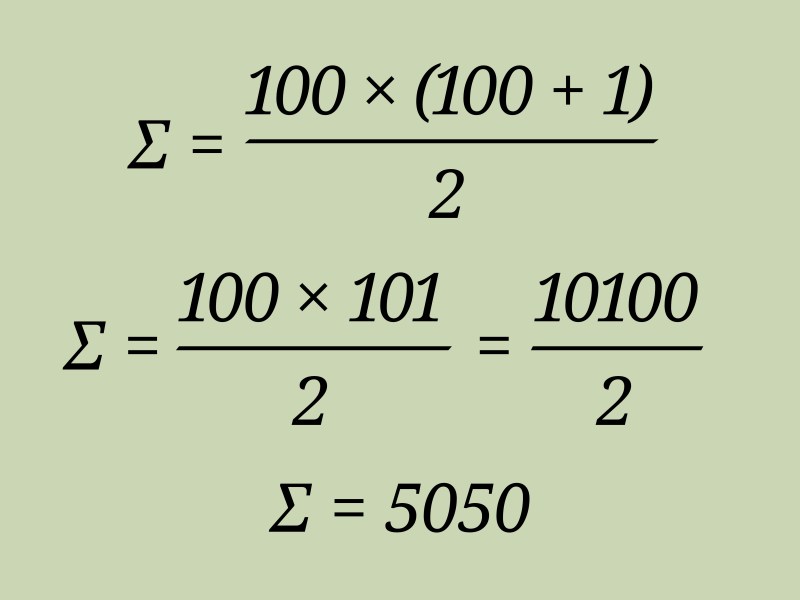Jumlah 14 Suku Pertama Dari Barisan Bilangan Ganjil Adalah – Pemberitahuan Penting Pemeliharaan Server Terjadwal (GMT) Minggu, 26 Juni, mulai pukul 02.00. – 08:00 M. . Situs ini akan tidak aktif selama waktu yang ditentukan!
Pola Bilangan Mata Pelajaran: Matematika Modul: 1 Kelas/ Semester: VIII / Tahun Tunggal: 2020/2021 Pendahuluan 1. Tujuan Setelah menyelesaikan modul ini, mahasiswa diharapkan mampu memahami, menjelaskan dan menggunakan permasalahan terkait. Jumlah akar pangkat dan bentuk. 2. Cara penggunaan modul Secara umum cara penggunaan modul dalam setiap kegiatan pembelajaran selalu menyesuaikan dengan situasi penyajian materi. Untuk menyelesaikan paket modul ini, siswa diharapkan menyelesaikan seluruh kegiatan, yaitu: mempelajari bahan pelajaran, mengerjakan kegiatan tugas/soal dan mengembalikan tugas yang telah selesai. Kegiatan Pembelajaran Kegiatan 1: Pola bilangan Memahami barisan bilangan Pada modul ini Anda akan mempelajari pola barisan bilangan. Pertama, perhatikan baik-baik teks berikut. Jika bilangan-bilangan diberi nama menurut aturan tertentu, maka bilangan-bilangan tersebut akan membentuk suatu barisan. Setiap angka disebut istilah. Hal ini menjadi lebih jelas jika kita melihat contoh: Contoh 1 1, 3, 5, 7, … merupakan deretan bilangan aturan, setiap suku ditambah 2 untuk mendapatkan suku berikutnya. 1 adalah suku pertama 3 adalah suku kedua 5 dari 1 + 2 adalah 3 + 2 7 adalah suku ketiga 5 + 2 adalah suku keempat Contoh 2 2, 5, 8, 11, … adalah suku berikutnya Aturan a didapat deretan angka yang tiap suku ditambah 3. 2 adalah suku pertama 5 adalah suku kedua dan 2+3 sampai 8 adalah suku ketiga yaitu 5+3 MGMP Matematika SMP Cab. Modul Matematika Kelas VIII Semarang 2020 1
Jumlah 14 Suku Pertama Dari Barisan Bilangan Ganjil Adalah
11 itu suku keempat dari 8 + 3, gimana caranya mudah kan? Sekarang lakukan latihan berikut. Latihan Menentukan aturan barisan bilangan berikut a. 3, 6, 9, 12,……b. 3, 6, 12, 24, ……. C. 100, 96, 92, 88, …… Jika jawaban anda kurang benar, coba ulangi sampai anda mendapatkan hasil yang baik. Jawaban latihannya dapat dikaitkan dengan jawaban di bawah ini. Jawaban praktis a) 3, 6, 9, 12…. Aturannya adalah menambahkan tiga untuk mendapatkan suku berikutnya. Cara Selanjutnya Untuk memperoleh suku berikutnya…. Metode Suku pertama 3 24 Suku kedua 2×3 =6 12 Suku ketiga 2×6 = 12 6 Suku keempat 2×12 = 24 3 c) 100, 96, 92, 88, … untuk mendapatkan 4 Aturannya adalah mengurangkan Suku berikutnya Caranya 100 – 4 = 100 100 = 96 96 Suku ke-1 96 – 4 = 92 92 Suku ke-2 92 – 4 = 88 88 Suku ke-3 Suku ke-4 Coba ulangi latihan berikut: …. Tuliskan dua suku barisan bilangan berikut a) 0, 3, 6, 9, 12, …, …. b) 2, 6, 10, 14, …., ….. c ) 3, 6, 12, 24, …, …. d) 100, 96, 92, 88, …, …. MGMP Matematika Sekolah Menengah Distt. Modul Matematika Kelas VIII Semarang 2020 2
Soal & Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 22 23 ‘cara Hitung Pola Bilangan’
Anda sudah mengetahui aturan dari latihan sebelumnya, jadi jawabannya adalah: a) 0, 3, 6, 9, 12, 15, 18; Dua suku berikutnya adalah 15, 18 b) 2, 6, 10, 14, 18, 22,; Dua suku berikutnya adalah 18, 22 c) 3, 6, 12, 24, 48, 96,; Dua suku berikutnya adalah 48, 96 d) 100, 96, 92, 88, 84, 80; Dua bilangan berikutnya adalah 84 dan 80. Dari contoh dan latihan yang telah anda pelajari, saya harap anda memahami apa yang dimaksud dengan barisan bilangan. Selanjutnya saya akan memberikan contoh lain barisan bilangan yang tersusun dalam segitiga Pascal. 1 11 121 1331 14641 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 Perhatikan gambar segitiga Pascal di atas. Di sana Anda akan melihat 2 diagonal. Setiap diagonal membentuk barisan numerik. Urutannya adalah: 1, 3, 6, 10, 15, 21. Aturannya adalah: Suku pertama 1 = 1 Suku kedua 1+2 = 3 = 1+2 Suku ketiga 3+3 = 6 = 1+2+ 3 Keempat suku 6 + 4 = 10 = 1 + 2 + 3 + 4 Suku kelima 10 + 5 = 15 = 1 + 2 + 3 + 4 + 5 Suku keenam 15 + 6 = 21 = 1 + 2 + 3 + 4 + 5 + 6 Angka Kisaran ini memiliki pola yang dapat digambarkan sebagai segitiga. Beberapa barisan bilangan dapat ditampilkan dengan cara lain, yaitu dalam bentuk pola bilangan, perhatikan contoh berikut: Contoh: Barisan bilangan asli: 1, 2, 3, 4, . . . . Misalnya anda dapat menyusun barisan bilangan real dari biji atau batu kecil, cobalah sendiri. • , • • , • • • , • • • •, … Selanjutnya kita dapat membuat barisan bilangan kuadrat. MGMP Matematika SMP Negeri. Semarang 2020 3 Modul Matematika Kelas VIII
Apa bentuk garisnya? Apakah hasilnya sama dengan gambar di bawah ini? ••••••••• • … • •••••••••••••••••••••••••••• • Untuk membentuk deret angka, kamu dapat berhitung dari jumlah butir yang Anda miliki. Dapat juga dikatakan barisan 1, 4, 9, 16, ….. merupakan barisan bilangan asli pangkat dua. Mengapa disebut demikian? ….. Alasan 1, 4, 9, 16, ….. Aturan 12, 22, 32, 42, …… Sekarang bisakah kamu dan temanmu menyusun batu atau biji kecil dalam sebuah segitiga? Jika sudah sesuaikan dengan pengaturan pada gambar di bawah ini. • • • … ••••••••••••••••••••••• Urutan 1, 3, 6, 10,…. Dengan menggunakan contoh dan cara penyusunan batu kecil atau besar, Anda telah melihat banyak pola yang dapat disusun dalam urutan numerik. Dengan begitu, Anda pasti bisa memahami uraian materi yang telah Anda pelajari. Sekarang cobalah latihan berikut. Susunlah dari butirannya terlebih dahulu, lalu Anda bisa menguraikannya di buku dan dilanjutkan dengan 2 pola berikutnya. •••••••••••••••••• •••• Jika sudah selesai, cocokkan hasil Anda dengan jawaban di bawah ini. Jika hasilnya belum semuanya benar, ulangi lagi. Jawabannya adalah OOOOOOO OOOOO OOOOOOO OOOO OOOOOOO OOOOOOO OOO OOOO OOOOOOO OOOOOOO O O, O O O, O O O O, O O O O O, O O O O O O Jika diperhatikan lebih dekat, barisan tersebut mempunyai pola persegi panjang. MGMP Matematika SMP Negeri. Modul Matematika Kelas VIII Semarang 2020 4
Barisan tersebut adalah: 2, 6, 12, 20, 30. Suku pertama = 2 = 2×1 Suku kedua = 6 = 3×2 Suku ketiga = 12 = 4×3 Suku keempat = 20 = 5×4 Suku kelima = 30 = 6×5 Tugas 1 1. Tentukan aturan barisan bilangan berikut a. 2, 4, 8, 16, …b. 60, 55, 50, 45,…c. 1, 10, 100, 1000,…d. 64, 32, 16, 8 2. Tuliskan dua suku berikutnya dari deret bilangan di bawah a. 1, 5, 9, 13,…,…b. 5, 8, 11, 14,…,…c. 0, 1, 4, 9, 16…,…d. 2, 4, 8, 16,…,…e. 1, 3, 6, 10,… F. 1 , 2 , 3 , 4 , 5 ,…. 2 5 9 14 20 3. Isilah titik-titik berikut hingga membentuk barisan bilangan yang benar. A.23, 20,…14, 11, ….., ……. B.12, 24, ….. 96, ….., 384 c. 8,……12,14,….,18d. 56, …., 64, 68, 72, ……, ……. 4. Gambarlah pola titik-titik untuk menunjukkan a. Barisan bilangan kuadrat adalah 1, 4, 9, 16, …… b. Barisan bilangan kuadrat 2, 6, 12, 20, …. Kerjakan tugas 1 ini sebaik mungkin. Jika sudah selesai, Anda dapat mencocokkan jawaban Anda dengan kunci tugas. Jika ada jawaban yang salah selama pengerjaan, pelajari kembali materi kegiatan ini. Anda kemudian dapat memulai mempelajari aktivitas kedua. MGMP Matematika SMP Negeri. Semarang 2020 5 modul matematika kelas VIII
Kegiatan 2: Barisan Aritmatika Barisan Aritmatika Setelah mempelajari Kegiatan 1, anda pasti dapat memahami berbagai macam barisan bilangan. Karena terdapat aturan tertentu untuk berbagai barisan bilangan tersebut, maka disebut barisan aritmatika. Coba perhatikan interval berikut: a. 1, 3, 5, 7, …b. 3, 7, 11, 15,… c. 20. Barisan yang mempunyai sifat seperti ini disebut barisan aritmatika dan selisih dua suku yang berurutan disebut selisih yang bertanda (b) dan suku pertamanya adalah (U1 ) * Pada barisan pertama : 1, 3, 5, 7 , …. Selisih = 3 – 1 = 5 – 3 = 7 – 5 Jadi b = 2, a = 1 * Pada baris kedua : 3, 7, 11, 15, …. Selisih = 7
English For Mathematics
Barisan bilangan kelas 8, bilangan ganjil dan genap adalah, barisan bilangan dan deret, suku barisan, pengertian barisan bilangan, cara mencari suku pertama barisan geometri, pola dan barisan bilangan, rumus jumlah suku ke n barisan aritmatika, rumus jumlah n suku pertama deret geometri, barisan bilangan fibonacci, bilangan ganjil, bilangan ganjil adalah